2.- Escribir un programa que calcule el producto escalar de dos vectores de enteros. Si v y w son los vectores y n su tamaño, el producto escalar se calcula como el sumatorio de V(i)*W(i)
3.- Escribir un programa que calcule el valor mínimo y máximo de un vector de enteros.
4.- Programa que imprime un cuadrado latino de orden n. El cuadrado latino de orden n es una matriz cuadrada en la que cada casilla está ocupada por uno de entre n símbolos de tal modo que cada uno de ellos aparece exactamente una vez en cada columna y en cada fila. Para simplificar el problema podemos ver el cuadrado latino de orden n como una matriz cuadrada en la que su primera fila contiene los n primeros números naturales y cada una de las siguientes n-1 filas contiene la rotación de la fila anterior un lugar a la derecha.
5.- Desarrolla una función que calcule la transpuesta de una matriz dada de orden nxm. Una matriz es transpuesta de otra si su elemento aij se corresponde con el elemento aji de la anterior.
6.- Escribe una función que imprima el contorno de una matriz de orden nxm, esto es, que visualice el borde de la misma dejando hueco el lugar de sus valores interiores.
7.- Escribe un programa que sume los valores de las dos diagonales de una matriz cuadrada de orden n.
8.- Escribe un programa que cree un cuadrado mágico de orden n. Un cuadrado mágico es una matriz cuadrada en la que todas sus filas, columnas y diagonales suman lo mismo.
NOTA: Utiliza el siguiente algoritmo voraz (sólo sirve para órdenes impares) y luego inténtalo con backtracking recursivo para cualquier orden, par o impar.
RESUMEN del algoritmo:
a) Se coloca el 1 en la posición central de la primera fila
b) Desde 2 hasta el resto de números del cuadrado mágico (n x n), se comprueba si el número colocado con anterioridad es múltiplo de n. Pueden suceder dos cosas:
b.1) Si es múltiplo de n, el número se coloca en la misma columna de la siguiente fila.
SOLUCIÓN VORAZ PARA ORDEN IMPAR
b.2) Si NO es múltiplo de n, el número se coloca en la celda de la fila anterior y columna posterior, con la peculiaridad de que la fila anterior a la primera es la última y la columna posterior a la última es la primera, o sea, la matriz es circular.
SOLUCIÓN BACKTRACKING PARA ORDEN CUALQUIERA
9.- Escribe una función que compruebe el valor o valores que más se repiten en un vector (moda). La función, exactamente, devolverá el número de modas que encuentre, esto es: si ningún valor se repite devolverá cero, si hay sólo una moda devolverá uno y si hay más de un valor con el mismo número de repeticiones nos dirá cuantos valores hay con la misma frecuencia. El valor o valores de la/s modas se almacenará en un vector a modo de parámetro de salida donde cada celda será un par (valor que se repite, frecuencia de repetición) Ejemplo:
{4, 6, 5, 8, 3} -> modas: 0; vector solución = {}
{4, 5, 1, 4, 4} -> modas: 1; vector solución = {(4,3)}
{3, 4, 3, 5, 4} -> modas: 2; vector solucion = {(3,2) , (4,2) }
10. El cuadrado de Vigenère es un método criptográfico para cifrar mensajes cuya clave es la tabla que se muestra tras este enunciado así como una palabra que se escribe tantas veces como sea preciso hasta cubrir la longitud del mensaje original y se trunca al final si fuese necesario. De esta forma, cada letra del mensaje cifrado se obtiene mediante la intersección de la columna cuya primera letra es la original con la fila cuya primera letra es la letra clave correspondiente. Con un ejemplo se comprenderá mejor: supongamos que la palabra clave es DIA, y que queremos codificar la palabra RAREZAS, entonces se tiene la siguiente situación:
R A R E Z A S
D I A D I A D
La letra clave correspondiente a la primera R es la letra D, entonces la letra que se genera mediante este cifrario es la letra U, ya que la intersección de la columna que empieza por la letra R con la fila que empieza con la letra D es la letra U. De esta forma la palabra codificada será:
UIRHHAV
Crea dos funciones C++ para codificar y decodificar mensajes con este procedimiento.
11.- La rejilla de Cardano es un método criptográfico renacentista. Consistía en una rejilla perforada de tal forma que al rotarla 90º hasta 3 veces, conseguía dejar al descubierto las distintas celdas de una tabla, sin que en ningún momento se solapen los cuadros perforados en la posición original y las siguientes giradas un cuarto de vuelta. Esta característica permite ir rellenando la rejilla y cuando se acaban los huecos perforados se gira 90º para seguir rellenando la tabla, así hasta un total de 3 giros. Si sobran huecos al final se dejan en blanco. Retirada la rejilla perforada nos queda el mensaje cifrado en una tabla. Para decodificarlo se superpone de nuevo la rejilla y se va girando 90º hacia el mismo lado que se hizo la codificación. En esta infogafría se muestra un claro ejemplo:
Crea dos funciones C++ para codificar y decodificar mediante este método usando la misma rejilla del ejemplo gráfico.
12.- Desarrolla un programa que permita imprimir matrices caracol. Las matrices caracol son matrices cuadradas de orden n que almacenan los n x n primeros números naturales, empezando en 1, en forma de espiral como se muestra en la salida de pantalla siguiente:
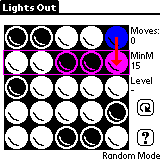
13.- Crea un programa que implemente en modo consola el popular juego Lights Out (¡Luces Fuera!). Este juego consiste en un tablero de dimensiones 5 x 5 en el que sus celdas son "bombillas" que pueden estar apagadas o encendidas. El usuario puede seleccionar una celda para cambiar su estado, de apagada a encendida o viceversa. Al mismo tiempo, también cambian de estado las celdas vecinas (las de encima, debajo, izquierda y derecha). El tablero inicial se generará de forma aleatoria. El objetivo del juego es conseguir que se apaguen todas las luces del tablero. Para entender el mecanismo del juego puedes visitar esta web donde podrás probar una versión gráfica en flash.
Mejoras propuestas:
- Adapta el TDA lista desarrollado en clase de teoría para poder ir registrando las celdas en las que el usuario va efectuando las "pulsaciones". De esa forma, podrás ofrecer una opción de deshacer uno o varios pasos para retomar un estado anterior del tablero.
- Habilita una opción para que la computadora resuelva automáticamente el puzzle. Para resolverlo de forma sistemática debes llevar a cabo los siguientes pasos:
a) "Pulsa" de derecha a izquierda, en la segunda fila, todas las bombillas que encima (en la primera fila) tengan alguna luz encendida. Esto hará que se apaguen todas las luces de la primera fila.
b) "Pulsa" de derecha a izquierda, en la tercera fila, todas las bombillas que encima (en la segunda fila) tengan alguna luz encendida. Esto hará que se apaguen todas las luces de la segunda fila.
c) Repite este proceso de los pasos a) y b) pero con las filas cuarta y quinta.
d) Si en la última fila han quedado luces encendidas y, por lo tanto, no se ha resuelto el juego, hay que observar el patrón en código binario resultante (luz encendida - 1, luz apagada - 0). Ahora busca en la tabla de la izquierda dicho patrón. Pues bien, el patrón de activación asociado al mismo, en la tabla de la derecha, es el que hay que pulsar al principio del juego antes de empezar el proceso descrito en los pasos a) b) y c) para que en la última fila no queden luces encendidas y por lo tanto se resuelva el puzzle. La computadora podría hacer el ensayo sobre una copia del tablero para descubrir el patrón y luego llevar a cabo el proceso final de resolución en una sola pasada de arriba abajo.
17 -> 24
10 -> 18
28 -> 8
7 -> 2
22 -> 1
13 -> 16
27 -> 4















No hay comentarios:
Publicar un comentario